Valóban elliptikus pályán mozognak a bolygók a Naprendszeren belül, a tér viszonylatában?

 Az ember, mivel a Földön él, már kezdettől figyeli a környezetét a Föld viszonylatában. Néha mondja is: tudom, mert láttam! Vajon az az igaz, amit látsz és ahogy látod?

Most csak arról beszélek, ahogy az eget, az univerzumot látta.

1, A Földről figyelve, észrevette, hogy a Nap és több égitest mozgása, egymással összefüggésben van. Így fedezte fel a bolygókat, de nem értette az összefüggés alapjait, ennek ellenére megalkotott egy matematikai összefüggést az események kiszámítására. A hosszú idejű megfigyelések elemeit papírra vetette és rájött, hogy a bolygók körpályán mozognak és epicikloidokat írnak le. Tehát nem látta az égen a epicikloidokat soha, csak ha kivetítette egy rajzon.

2, Kopernikusz rájött, hogy az egészet nem a Földről, hanem a Napról kell szemlélni, vagyis a Naphoz viszonyítva. Gyakorlatilag ezt nem teheti meg senki, ezért a mérések alapján adatokat gyűjtöttek, amelyet papírra vetve meg tudták állapítani, hogy a bolygók a Nap körül keringenek egy-egy körpályán, amelyet később Kepler, a pontosabb mérések alapján kijavított, elliptikusra. Egyik sem látott soha sem kör, sem elliptikus pályát az égen, csak kivetítve papíron. Erre a mozgási formára, már Newton megfogalmazott egy matematikai összefüggést, amit a mai napig használnak a gyakorlatban. Azonban nincs meghatározva, mi élteti a ciklusos mozgást, mert minden ciklusos mozgás impulzust (lőkést) igények minden periódusba.

3, Most jöttem én, aki hallotta, hogy a Nap nem áll, hanem kb. 220 km/s sebességgel halad az űrben. Hogyan lehetséges egy mozgó Nap körül, elliptikus pályán keringeniük a bolygóknak. Azt tudom, hogy mozgó pont köré nem lehet kört rajzolni körzővel. Mivel az égitestek útvonalát nem lehet követni szemmel, nem papírra vetítettem ki a mozgások nyomvonalait, hanem egy erre a célra írt, számítógépes programmal ábrázoltam. A program alkalmas a Kopernikuszi Naprendszer utánzására, úgy hogy az égitestek nyomát is lehet követni. (kiírja/kirajzolja, ha akarom ugyanúgy, ahogy azt a csillagászok tudják) A programot tovább fejlesztve tudom követni a bolygók pályájának útvonalát, akkor is, amikor a Nap mozgásba van. Ekkor derültek ki eddig ismeretlen dolgok. A Nap sebességétől függően a bolygók pályája nem egyforma. Ha a Merkúr pályája hurkot ír le, akkor már a következők egyre jobban követik a ciklois formát, egyre jobban elnyúlnak. Ha ciklois formára állítom a Merkúr pályáját, a többiek egyre jobban elnyúlnak a szinuszoid felé. Mivel az inga is cikloist ír le, a lengés alatt, megpróbáltam kiszámítani a bolygók keringési periódusát az ingatörvény alapján, amikor kiderült számomra, hogy ez egy az egyben egyezik az ismert értékekkel. A bolygó ingarúdja egyenlő a Naptól való távolsággal, s a gravitációs gyorsulása egyenlő a Nap gravitációjának az értékével a bolygó pályáján. Egy primitív kísérlettel próbáltam utánozni a jelenséget. Egy forgó ingát rögzítettem a kerékpár kormányának végére, előre lendítettem amikor elindultam. Egy bizonyos sebességnél az inga folyamatosan keringett a menetirányba. Van egy mozgásban levő húzóerő központ, van az inga tömege és a Föld gravitációja.

Innen jött az ötlet, hogy határozzam meg egy normál ciklois, pozitív-negatív hullámának arányát. Kiderült, hogy az arány nem függ a gördülő kör sugarától, tehát a Nap-bolygó távolságtól. Ennek értéke 4,5087. Azt sem feltételeztem, hogy egy bolygó a térben követhet egy ciklois pályát, mert a hirtelen irányváltást nem képes megtenni. Csináltam egy olyan ciklois utánzatot, amelyben az út hosszát megszoroztam 4,5087-el.

 

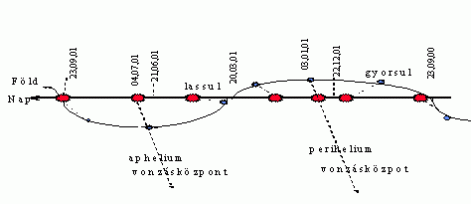    Fig.1. Megközelítőleg így néz ki a Nap-Föld térbeli mozgása (2000-2001 év)

Így kaptam meg a szinuszoid pályaformát és a csúszó-guruló út hosszát. Kiindulva a legközelebbi bolygó adataiból, amely szinuszoid pályájú kell legyen, kiszámítottam a megtett utat az ismert keringési periódus alapján, s megtaláltam a Merkúr átlagsebességét a térben, amely 215,736 km/s. Ez nagyon megközelíti az ismert adatot. A Merkúr szinuszoid pályájának átlagsebessége egyenlő a Nap sebességével. Azért mondok átlagsebességet, mert a szinuszoid pályán a sebesség változó. Ezzel a Nap sebességgel kiszámítottam az összes bolygó adatait, amelyet grafikuson ábrázolva egy exponenciális görbét kaptam. Ez vonatkozik a bolygók minden adatára, kivéve a tengely körüli forgásperiódust, amely nem exponenciális. Bármely bolygó távolságot megváltoztatom, a

 

 

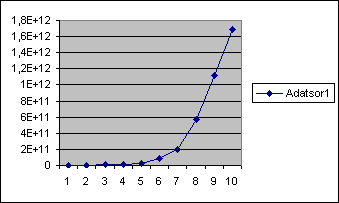
Fig.2 A bolygók periódusa alatt a Nap által megtett út exponenciálisan növekedik.

grafikon exponenciális vonalától eltér. A Plútó nem éppen esik egybe az exponenciális görbével. Ez azt jelenti, hogy nem keringhet folyamatosan azonos pályán égitest, amely kívül esik az exponenciális grafikon vonalán. A Föld évi úthosszát elosztom a Hold egy fordulat alatt megtett útjával és megkapom, hányszor járja körbe a földet a Hold egy évben (13,36). Úgy néz ki, hogy a Naprendszer minden égitestének átlagsebessége azonos egy adott időszakban, mert a Nap is évmilliókban számítva szinuszoid pályán halad. Itt is, mint a kísérletben, van a mozgó-húzó tömeg a Nap, az ingarúd – amely a gravitációs vonzerő - végül a bolygó tömegével és a Galaxis központi gravitációjával (másképp nem térne vissza a bolygó). Amikor a bolygó-Nap-galaxisközpont egy vonalban van, akkor a Nap-galaxis gravitáció a perihéliumban összegződik és a aphéliumban kivonódik. Ezért lesz elliptikus a pálya a Kepleri elv szerint, valamint a Merkúr perihélium pontjának vándorlását az okozza, hogy a Nap pálya és a Nap-galaxisközpont vonala által bezárt szög folyamatosan csökken a jelenlegi állapot szerint. Ez nem volt mindig így és nem lesz mindig így.

A Hold, Merkúr és Vénusz körforgási és keringési periódusa azonos, ami azt jelenti, hogy csúszó gurulásból adódik, de az is megfigyelhető, hogy minél több Holdja van egy bolygónak, annál gyorsabb a tengely körüli forgása.

Egy gyakorlati bizonyíték arra nézve, hogy a bolygók szinuszoid pályán keringenek, a Föld árapály jelensége. Legalább is nyílt vizeken az évi vízszint grafikonnak szinuszoid formája van. Az árapály vízszintje a legkisebb, amikor a Föld sebessége a legkisebb – apogeu - és fordítva - perihelium, a tehetetlenség miatt.

 

Csináltam egy kísérletet egy közönséges ingával, amelyet egy kerékpár kormányának külső végére függesztettem fel és egy bizonyos sebességnél (nem tudtam mérni), az ingát meglenditve előre, folyamatosan keringet a kormánykörül, de a térben szinuszoid pályát írt le. Tehát kell egy húzó erő, minden ciklusban. A bolygók a húzóerőt az apheliumból indulva kapják meg. egészen a priheliumig. Utána tehetetlenség és gravitáció adja meg az útvonalát.

 

 Románia, Olasztelek, kis Székely falu                                 Szőcs Sandor

 

 

 

 

 

 

 

 

 

 

 

R 

 

 

 

Oldal: Copernicus után
Új fizikai elvek a Naprendszerről, a Doppler-elvről, információtárolásról - © 2008 - 2025 - van-uj.hupont.hu

A weblap a HuPont.hu weblapszerkesztő használatával született. Tessék, itt egy weblapszerkesztő.

ÁSZF | Adatvédelmi Nyilatkozat